[논문 요약/리뷰] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

 

Author : Ioffe, Sergey, and Christian Szegedy.
Journal : ICML 2015
Published Date : 2015년 2월 11일
Keyword : Batch Normalization

---

Abstract

• 학습 하는 동안 입력 데이터는 네트워크 레이어를 거치며 분포가 계속 변화한다. 레이어의 파라미터가 역전파에 의해 계속해서 바뀌기 때문이다.
• 입력 분포가 변화하는 게 문제가 되는 이유는, 각 레이어가 새로운 입력 분포에 계속 적응해야 하기 때문이다.
• 입력 분포가 계속해서 변화하는 것을 Covariate Shift(공변량 변화)라고 한다.
• 이는 일반적으로 Domain Adaptation을 통해 처리했으나, 본 논문에서는 “Batch Normalization”으로 이 문제를 완화한다.

---

Problems

SGD Training Mechnism

• SGD(Stochastic Gradient Descent)는 입력 데이터가 $\mathrm x_{1 \dots N}$인 경우, 아래의 Loss($\ell$)를 최소화하는 $\Theta$를 찾는 것으로 정의된다.

$$\Theta = \argmin_\Theta \frac{1}{N}\sum^N_{i=1} \ell (\mathrm x_i, \Theta )$$

• 배치 크기가 m인 경우, 가중치의 그래디언트는 아래와 같이 미분값으로 계산된다.

$$\frac{1}{m}\frac{\partial \ell (\mathrm x_i, \Theta)}{\partial \Theta}$$

---

Distributions of layers’ Inputs

$$\ell = F_2(F_1(u, \Theta_1), \Theta_2)$$

• 임의의 변환 $F_1, F_2$ 가 있다고할 때, 파라미터 $\Theta_1, \Theta_2$는 Loss($\ell$)를 최소화하게끔 학습된다.
• 이 때 $\mathrm x = F_1(u, \Theta_1)$를 $F_2$의 입력으로 보면 아래와 같이 다시 정의할 수 있는데,

$$\ell = F_2(\mathrm x, \Theta_2)$$

• 입력 데이터 $\mathrm x$에 대한 독립적인 네트워크 $F_2$를 학습시키는 것과 동일하게 볼 수 있다.
• 즉 레이어에 따른 입력 데이터 $\mathrm x$의 분포가 일정할 수록 학습되는 파라미터도 크게 변화하지 않아도 되기때문에 효율적이다.

---

Gradient Vanishing

• 가중치 소실 문제는 활성화 함수 시그모이드의 입력값이 커지게되는 경우 발생한다.

Sigmoid 활성화 함수

• 시그모이드 $g(x) = \frac{1}{1+\exp(-x)}$는 위와 같은 형태로, $|x|$가 커지면 그래디언트(미분)은 0에 수렴하게 된다.
• 역전파 수행 시 각 파라미터에 그래디언트가 더해지면서 업데이트가 되는데, 0으로 수렴해버린 그래디언트 때문에 파라미터가 더 이상 업데이트되지 않는 문제가 Gradient Vanishing이다.
• 이 문제를 해결하기 위해 활성화 함수를 ReLU를 교체하거나, 가중치 초기화를 적용한다.
• 하지만 입력 데이터의 분포를 일정하게 유지하면 활성화 함수의 입력값이 포화(Saturation)되는 것을 방지하여, 훈련이 더 가속화 될 것이다.

---

Whitening

• Whitening(백색화)란 평균을 0으로 만들고 분산을 1로 조정하는 변환을 말한다.
• 각 레이어의 입력에 대해 모두 Whitening을 수행하여 입력의 평균과 분산을 모두 같게할 수 있다.
• 하지만 이 방법의 문제는 학습을 무효화할 수 있다는 것이다.
• 예를 들어 입력 데이터 $\mathcal X={x_{1\dots N} }$이 있다고하자. $x = u + b$로, $u$는 전 단계 레이어의 출력, $b$는 bias이다.
• 이 때 정규화를 위해 원래의 입력 데이터에서 평균을 빼면 $\widehat x = x - E[x]$이 된다.
• 여기서 $E[x]$가 $b$와 독립적이라고 가정하고, 업데이트된다고 해보자.

$$\widehat x = u + (b+\Delta b) - E[u + (b+ \Delta b)] = u + b - E[u+b]$$

• 그렇다면 위와 같이 $\Delta b$가 사라지는 상황이 만들어질 수도 있게 된다.
• 따라서 Whitening은 학습의 효과를 없앨 수도 있는 문제가 있다.

---

Contributions

• 훈련 과정에서 내부 노드들 간 분포 변화 현상을 내부 공변량 변화(Internal Covariate Shift)라고 한다.
• 본 논문에서는 Batch Normalization을 적용하여 이 문제를 완화시켜서 훈련을 가속화한다.
• Batch Normalization은 각 층의 입력값들의 평균과 분산을 일정하게 유지해서 네트워크가 포화되는 것을 방지하는 규제(Regularization) 역할을 한다.

---

Methods

• 각 레이어의 입력 데이터를 평균이 0이고 분산이 1인 분포로 정규화하는 Whitening과는 다르게, Batch Normalization은 전체 데이터셋을 기준으로 평균과 분산을 계산한다.
• 예를 들어 $d$차원 벡터 $\mathrm x = (x^{(1)}\dots x^{(d)})$가 있을 때, 전체 데이터셋을 기준으로 각 차원을 다음과 같이 정규화한다.

$$\widehat x^{(k)} = \frac{x^{(k)}-E[x^{(k)}]}{\sqrt {Var[x^{(k)}]}}$$

• 하지만 단순히 각 층의 입력을 정규화하는 것만으로는 선형 영역으로 제한되어 표현력이 약화될 수 있다.
• 이게 무슨말이냐면, 정규화를 거치고나면 입력값들은 대부분 0에 가까이 몰려있을 것이다. 그런데 Sigmoid 활성화 함수는 0 근처에서는 선형성을 가지기 때문에, 비선형성이 억제된다는 말이다.
• 이를 해결하기 위해 두 개의 학습 가능한 파라미터 $\gamma^{(k)}, \beta^{(k)}$를 도입하여 정규화된 값을 스케일링하고 이동(Shift)시킨다.

$$y^{(k)} = \gamma^{(k)}\widehat x^{(k)} + \beta ^{(k)}$$

• 여기서 $\gamma^{(k)} = \sqrt {Var[x^{(k)}}, \beta^{(k)}=E[x^{(k)}]$인 경우, 원래 값을 복원할 수 있다.
• 만약 미니 배치 단위로 학습되는 경우, 미니 배치를 기준으로 평균과 분산을 구해 정규화한다.
• Batch Normalization의 알고리즘은 아래와 같다.

Batch Normalization 알고리즘

 

 

• 더 자세하게 들어가면, 역전파를 통해 가중치의 그래디언트를 계산하기 위해서는 Batch Normalization을 적용한 결과가 미분 가능해야한다.
• 논문에서는 Chain rule을 통해 미분 가능함을보인다.

Batch Normalization 연산의 미분 가능성

 

 

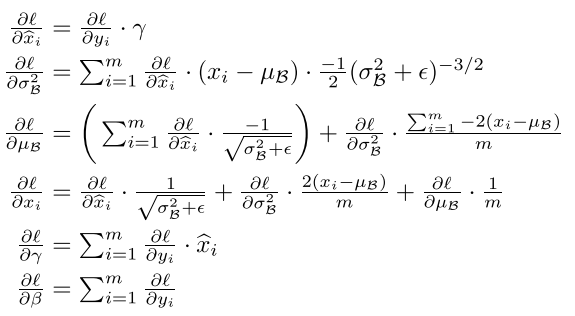
• 이제 Batch Normalization의 마지막 단계로, 추론에서 어떻게 활용되는지 알아야한다.
• 당연히 추론 단계에서는 학습을 하지 않기때문에, 이미 학습이 완료된 $\gamma, \beta$를 사용한다.
• 학습 중에, 미니 배치에 대한 평균과 분산도 이동 평균(Moving Average)으로 계산하여, 전체 데이터셋의 정보를 반영하게끔 조정한다.

Training, Inference 단계에서 Batch Normalization의 차이

• 학습 동안 조정된 BN 파라미터들을 추론 단계에서는 Frozen한 후 사용한다.

---

Experiment

Batch Normalization의 효과

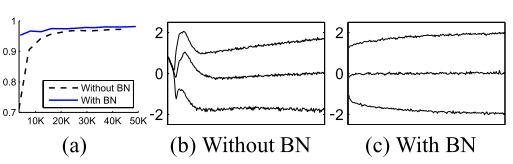
• (a)에서 BN이 적용된 경우, 더 빠르게 수렴되는 것을 확인할 수 있다.
• (b), (c)에서는 BN을 사용한 경우가 더 안정적으로 학습이 되는 것을 보여준다.

 

Batch Normalization 적용 성능 비교

• Steps to 72.2%는 정확도가 72.2% 까지 도달하는데 걸린 학습 Step을 의미한다.
• BN을 더 많이 적용할수록, Step이 더 짧아지고 Max Accuracy도 증가한다.

---

Conclusion

• Batch Normalization은 Internel Covariate Shift를 완화하여 훈련 속도를 높인다.
• 또한 비선형성 이전에 적용되어 활성화 값의 분포를 안정화시키고, 모델이 더 빠르게 수렴하도록 돕는다.