Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 이미지 필터링
- mobilenetv1
- 원격 학습 안끊기게
- google summer of code
- TransFuser
- gsoc
- 에지 검출
- object detection
- blip-2
- clip
- 논문 요약
- referring expression segmentation
- res
- 객체 검출
- Object detection article
- 엔트로피란
- 딥러닝 엔트로피
- E2E 자율주행
- 딥러닝 목적함수
- vlm
- 1차 미분 마스크
- gres
- gsoc 후기
- gsoc 2025
- 논문 리뷰
- grefcoco dataset
- grefcoco
- res paper
- transfuser++
- clip adapter
Archives
- Today
- Total
My Vision, Computer Vision
[논문 요약/리뷰] LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS 본문
LoRA: Low-Rank Adaptation of Large Language Models
An important paradigm of natural language processing consists of large-scale pre-training on general domain data and adaptation to particular tasks or domains. As we pre-train larger models, full fine-tuning, which retrains all model parameters, becomes le
arxiv.org
Journal : ICLR 2022
Published Date : 2021년 6월 17일
Keyword : LLM, RANK
Abstract
- 모델의 크기가 커질수록, 모델의 모든 파라미터를 재학습하는 Full Fine-tuning은 어려워진다.
- 본 논문에서는 LoRA(Low-Rank Adaptation)을 제안한다.
- Pre-trained 모델 가중치는 고정한 채로, 새로운 랭크 분해 행렬(Rank Decomposition Metrices)을 학습시킨다.
- LoRA는 GPT-3 175B 모델을 기준으로 파라미터 수는 약 10,000배 줄이고 GPU 메모리는 약 3배 감소시켰다.
Problem
- Large-scale로 사적학습된 LLM은 파인튜닝을 거쳐 Downtream 태스크에 적용되는데, 이 때 모델의 파라미터를 모두 업데이트하기 때문에, 비용이 크다는 단점이 있다.
- 이를 해결하기 위해 일부 파라미터만 학습시키거나 새로운 Adaptation 모듈만 학습시켰지만, 이는 Full Fine-tuning 성능에 미치지 못하거나 추론 지연(Inference Latency)를 초래한다.
- 따라서 본 논문에서는 선행 연구에서 입증된 Over-parameterized 모델이 실제로는 Low intrinsic dimension(낮은 내재 차원)으로 표현할 수 있다는 사실에서 가중치의 그래디언트 행렬 또한 “Low intrinsic rank”를 가질 것이라고 가정한다.
Contributions
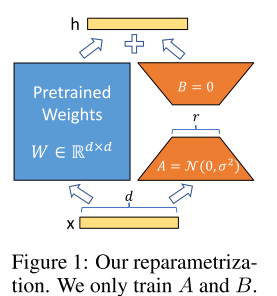
- 위 그림에서처럼 Pretrained Weights를 고정하고 대신 A, B 행렬만 학습하기 때문에, 훈련이 더 효율적일 뿐더러 Downstream 태스크에 따라 전환 가능하다.
- 모델 배포시 행렬 A, B를 고정된 Pretrained Weights와 결합하기 때문에, Inference Latency가 일어나지 않는다.
Rank란?
- 행렬의 계수(Rank)는 그 행렬이 표현할 수 있는 독립적인 벡터의 최대 개수를 의미한다.
- 여기서 독립은, 선형 독립을 말한다. 쉽게 말해, 행렬에서 선형 독립적인 행이나 열의 개수인 것이다.
- 예를 들어 아래와 같은 행렬이 있을 때,
$$ A = \begin{bmatrix}1, 2 \\ 2, 5 \\ 2, 4 \end{bmatrix} $$
- 세번째 행 [2, 4]는 첫번째 행 [1, 2]의 두 배로, 선형 결합이기 때문에 독립이 아니다.
- 그런데 두번째 행 [2, 5]를 보면 다른 어떤 행과도 선형 결합이 되지 않기때문에 독립이라고 할 수 있다.
- 따라서 A 행렬의 Rank는 2이다.
- Rank는 행을 기준으로 하든, 열을 기준으로 하든 같다.
Methods
Objective Approximation
- 사전학습된 Transformer 기반 Autoregressive Langauge Model(ex. GPT)을 $P_\Phi(y|x)$ 라 하자.
- 이제 사전학습된 가중치($\Phi_0$)로 모델을 초기화한 후 파인튜닝한다고 할 때, 가중치 업데이트는 $\Phi_0 + \Delta\Phi$로 이루어지며, Objective는 아래와 같다.
- $$ \max_\Phi \sum_{(x,y) \in \mathcal Z} \sum ^{|y|}{t=1} \log(P_\Phi(y_t|x, y{<t})) $$입력 텍스트 $x$ 와 이전 까지의 예측 $y_{<t}$ 가 주어졌을 때 다음 예측 $y_t$의 확률을 최대화하는 것이다.
- Fine-tuning의 단점은 학습되는 가중치의 차원 $|\Delta\Phi|$ 가 사전학습된 모델의 차원 $|\Phi_0|$ 과 같다는 것이다.
- 앞에서 언급했던 이 논문의 가정인 “모델뿐만 아니라 학습되는 가중치 또한 Low intrinsic rank를 가질 것이다.” 를 토대로 그래디언트 $\Delta\Phi$ 를 더 작은 크기의 파라미터 집합 $\Theta$ 로 학습되는 $\Delta\Phi(\Theta)$로 근사한다. 즉 $\Delta\Phi = \Delta\Phi(\Theta)$ 이 되는 것이다.
- 이렇게 변환된 Objective를 다시 쓰면 아래와 같다.
$$ \max_\Phi \sum_{(x,y)\in \mathcal Z} \sum^{|y|}{t=1} \log (p{\Phi_0+\Delta\Phi(\Theta)}(y_t|x,y_{<t})) $$
LoRA(Low-Rank Adaptation)
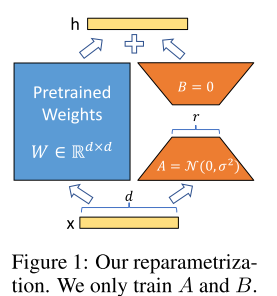
- 다시 말하지만 LoRA는 모델의 파라미터가 아닌 그래디언트를 근사하는 방법이다.
- 원래는 모델의 파라미터를 모두 파인튜닝해야 하지만, LoRA는 모델의 파라미터를 전부 고정시키고 그래디언트 행렬만 따로 학습시킨 후 원래의 가중치 행렬에 더함으로써 학습을 모방하는 것으로 볼 수 있다.
- 위 그림에서처럼 $d$ 차원의 입력 데이터 $x$를 $d$ 차원의 출력 벡터 $h$로 매핑하는 원래의 사전학습 가중치 행렬을 $W \in \mathbb R ^{d \times d}$ 라고하자.
- 원래의 학습이라면, 계산되는 그래디언트 행렬도 $W$ 와 같은 차원을 가져야하지만, LoRA는 두 개의 행렬 A, B로 쪼갠다.
$$ h = W_0x + \Delta W x = W_0x + BAx $$
- 각 행렬의 차원은 $A \in \mathbb R^{r\times d}, B\in \mathbb R^{d\times r}$ 이고 $r \ll d$ 이다. ($r$ 은 보통 4이다.)
- Trainable Parameter가 $d\times d$에서 $2\times d\times r$ 로 감소한 것이다.
- 학습이 끝난 후, 최종 모델의 가중치는 $W = W_0 + BA$ 로, 사전학습된 가중치 $W_0$에 새롭게 학습된 저차원 그래디언트 행렬 $B, A$를 행렬곱한 후 더해준다.
- 따라서 추론 때에도 모델의 파라미터는 그대로이기때문에, Inference Latency가 발생하지 않는것이다.

- 이는 실험 결과에서도 확인할 수 있는데, 위 테이블은 GPT-2에 LoRA, AdapterL, AdapterH를 적용한 후 Inference Latency를 비교한 실험이다.
- AdapterL과 AdapterH는 Pre-trained 모델을 고정하고 Adapter 모듈을 학습시키는 방법이다.
- Trainable Paramter는 같지만 추론 시 원본 모델에 비해 파라미터가 증가한 Adapter 방식과는 달리, LoRA는 파라미터가 추가되지 않기때문에 Latency면에서 효율적이다.
Experiment

- Transformer 모델에 LoRA를 적용할 때 Ablation study이다.
- Transformer에는 Attention Layer에는 Query, Key, Value, Output에 해당하는 Fully Connected Layer $W_q, W_k, W_v, W_o$ 가 있다.
- 이 때 Trainable Parameter의 개수는 $\mathrm {Num}{\mathrm{Weight Type}} \times \hat L{LoRA} \times d_{model} \times r$ 이다.
- $\hat L_{LoRA}$ 는 LoRA가 적용되는 레이어의 총 개수이다.
- 이 논문에서는 q, v에 r=4로 적용하는 버전을 사용한다.
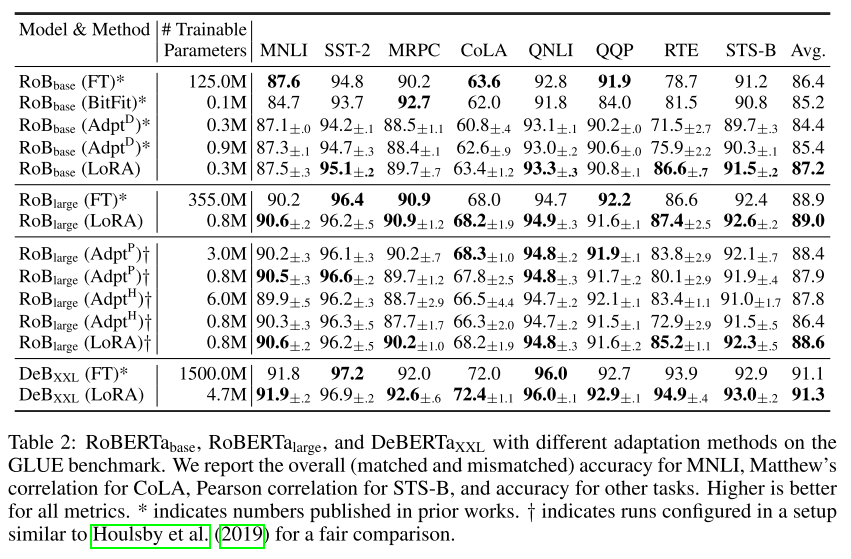
- 위 테이블은 RoBERT의 Base, Large, DeBERT의 XXL 버전에 여러가지 최적화 기법을 적용하여 실험한 결과이다.
- Trainable Parameter의 개수는 BitFit 방법이 가장 적지만 성능이 낮다.
- 전반적으로 LoRA를 적용했을 때 성능이 가장 좋고, Full Fine-tuning보다 더 높게 측정된다.
Conclusion
- Inference Latency를 발생시키지 않는 효율적인 학습 방법 LoRA를 제안한다.
- 향후 연구 방향으로는 LoRA와 다른 방법의 결합, LoRA를 적용할 가중치 행렬 탐색 방법 등이 있다.
Review
- 그래디언트를 학습하는 네트워크를 추가하여 학습을 모방하는 접근이 참신하다.
- 실험에 쓰인 LLM의 종류가 적다.
728x90




