| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- gsoc 2025
- 기계학습
- 이미지 필터링
- 논문 요약
- grefcoco
- referring expression segmentation
- res paper
- 원격 학습 안끊기게
- 딥러닝 엔트로피
- vlm
- gsoc 후기
- clip
- google summer of code
- 엔트로피란
- mobilenetv1
- 객체 검출
- 논문 리뷰
- 에지 검출
- Object detection article
- blip-2
- res
- gres
- object detection
- Segmentation
- 딥러닝 목적함수
- gsoc
- 1차 미분 마스크
- grefcoco dataset
- reparameterization
- clip adapter
- Today
- Total
My Vision, Computer Vision
[딥러닝 공부] Bernoulli Distribution, Laplace Distribution(베르누이 분포, 라플라스 분포) 본문
[딥러닝 공부] Bernoulli Distribution, Laplace Distribution(베르누이 분포, 라플라스 분포)
gyuilLim 2025. 1. 15. 15:46이번에는 가우시안 분포를 비롯하여 딥러닝 목적 함수에 자주 등장하는 분포들인 베르누이 분포와 라플라스 분포에 대해 알아보자.
베르누이 분포는 딥러닝 목적 함수에서 자주 등장하는 분포이며, Binary Cross Entropy에서 사용된다.
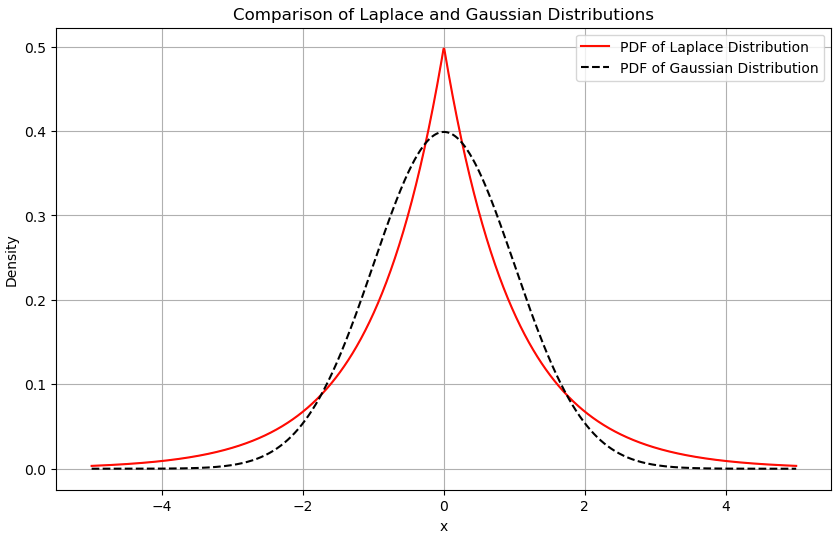
라플라스 분포는 가우시안 분포와 유사하게 뾰족한 종 모양으로 그려지는 분포이다.
Bernoulli Distribution(베르누이 분포)
이진 확률 분포의 일종으로, 두가지 가능한 결과 중 하나가 발생할 확률을 모델링한다.
발생할 수 있는 사건이 두 가지 경우밖에 없기때문에 이산 확률 분포이다.
따라서 PMF(Probability Mass Function, 확률 질량 함수)로 정의할 수 있다.
$$P(X=x) = p^x(1-p)^{1-x}, \quad x \in {0, 1}$$
위 식이 의미하는 것은 $x$가 1인 경우의 확률은 $p$, 0인 경우의 확률은 $1-p$라는 것이다.
베루누이 분포의 기대값은 $x=1$일 때 이므로,
$\mathbb E[X] = 0 \cdot (1-p) + 1 \cdot p = p$ 이고
분산은 다음과 같이 계산된다.
$Var(x) = \mathbb E[X^2] - (\mathbb E[X])^2 = p - p^2 = p(1-p)$
Laplace Distribution(라플라스 분포)
$$f(x) = \frac{1}{2b} \exp [\frac{-|x-\mu|}{b}]$$
라플라스 분포는 위와 같은 확률 밀도 함수로 표현된다.
가우시안 분포와 유사한 모양의 확률 밀도 함수이다.
범위는 $-\infty < f(x) < \infty$ 으로 모든 실수 범위이다.
평균 : $\mu$, 분산 : $2b^2$, 표준편차 : $\sqrt2 b$, 이 때 $b$는 스케일 상수라고도 함
라플라스 분포는 확률 밀도 함수기 때문에 적분했을 때 1이 된다. 절대값을 포함하기 때문에, 구간을 나누어서 적분해야한다.
$x \ge 0$ 의 경우
$$\int^\infty_0 \frac{1}{2b}\exp (\frac{x}{b})dx = \frac{1}{2b}\int^\infty_0\exp(-\frac{x}{b})dx = \frac{1}{2b}[-b \exp (-\frac{x}{b})]^\infty_0 = \frac{1}{2}$$
$x < 0$ 의 경우
$$\int^0_{-\infty} \frac{1}{2b}\exp (\frac{x}{b})dx = \frac{1}{2b}\int^0_{-\infty}\exp(-\frac{x}{b})dx = \frac{1}{2b}[b \exp (-\frac{x}{b})]^0_{-\infty} = \frac{1}{2}$$
두 구간에 대한 적분을 합치면 합이 1이 된다.
다음은 가우시안 분포와 라플라스 분포를 시각화한 그래프이다.
'공부' 카테고리의 다른 글
| [논문 리뷰/요약] LLaVA : Visual Instruction Tuning (1) | 2025.02.02 |
|---|---|
| [딥러닝 공부] KL Divergence와 Cross Entropy (0) | 2025.01.26 |
| [딥러닝 공부] 딥러닝 최적화4 - 하이퍼 파라미터 최적화 (5) | 2025.01.03 |
| [딥러닝 공부] 딥러닝 최적화3 - 규제 기법, 하이퍼 파라미터 최적화 (0) | 2025.01.03 |
| [딥러닝 공부] 딥러닝 최적화2 - 모멘텀, 적응적 학습률, 배치 정규화 (1) | 2025.01.03 |



