| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Object detection article
- 에지 검출
- blip-2
- res
- E2E 자율주행
- gsoc 2025
- res paper
- grefcoco dataset
- google summer of code
- 1차 미분 마스크
- 딥러닝 목적함수
- clip
- clip adapter
- 원격 학습 안끊기게
- 논문 요약
- referring expression segmentation
- gsoc
- gsoc 후기
- gres
- 논문 리뷰
- 이미지 필터링
- 딥러닝 엔트로피
- vlm
- object detection
- mobilenetv1
- grefcoco
- transfuser++
- 객체 검출
- 엔트로피란
- TransFuser
- Today
- Total
My Vision, Computer Vision
[딥러닝 공부] 딥러닝 최적화2 - 모멘텀, 적응적 학습률, 배치 정규화 본문
이 글은
『오일석, Machine Learning(기계 학습), 한빛아카데미(2017년)』
에서 공부한 내용을 토대로 작성되었다.
https://mvcv.tistory.com/42 이 글에서 이어집니다.
가중치 초기화
신경망의 가중치는 난수를 생성해 초기화하는데, 여기에서도 문제가 발생할 수 있다.
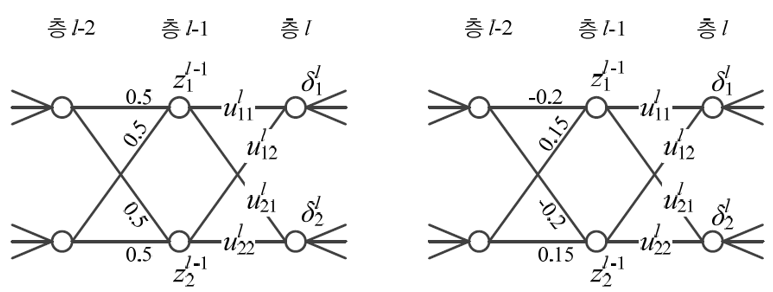
위 왼쪽 그림처럼 가중치가 모두 같은 값 0.5로 초기화되거나 오른쪽 그림처럼 같은 노드에 연결된 가중치가 같게 초기화될 수 있다.
이러한 경우를 대칭적 가중치가 발생했다고 한다. 이 문제가 발생하면 $z^{j-1}_1$과 $z^{j-1}_2$의 값이 같아지게 되고 가중치의 그래디언트도 같아진다.
따라서 $u$들이 모두 같은 값으로 갱신된다. 보통 이 문제를 해결하기 위해 두 가지의 가중치 초기화 방법을 사용한다.
$$r = \frac{1}{\sqrt{n_{in}}} \\ r = \frac{\sqrt6}{\sqrt{n_{in}+ n_{out}}}$$
위와 같이 r을 설정한 다음 구간 [-r, r]에서 난수를 선택하는 방법이다.
$n_{in}$ 과 $n_{out}$은 각각 하나의 노드로 들어오는 에지의 개수와 나가는 에지의 개수를 의미한다. 바이어스는 보통 0으로 초기화한다.
모멘텀
물리에서의 모멘텀은 질량에 속도를 곱한 값으로 나타내지만 신경망에서는 질량을 1로 가정하여 속도 벡터 v를 모멘텀으로 사용한다.
$\mathbf v$에 이전 가중치들을 누적하고, 비율 $\alpha$만큼 반영하여 매개변수 $\Theta$의 변화를 전체적으로 부드럽게 만들어주는 스무딩 효과가 나게 해준다.
$$\mathbf v = \alpha \mathbf v - \rho \frac{\partial J}{\partial \mathbf \Theta} \\ \Theta = \Theta + \mathbf v$$
첫번째 식을 살펴보면 v에 그래디언트를 계속 누적해나간다. 이 때, 이전 단계의 $v$를 $\alpha$만큼 반영한다. 즉 $\alpha$는 이전 그래디언트들의 가중치인 셈이다.
$\alpha$가 1이면 모든 단계의 그래디언트를 온전하게 반영한다는 의미이고 0이면 현 시점의 그래디언트만 반영하고 원래의 가중치 업데이트 수식과 같다.
보통 $\alpha$는 0.5, 0.9, 0.99를 사용하거나 처음에 0.5로 시작하여 점점 증가시켜 0.99에 도달하는 방법을 사용한다. 처음에는 그래디언트의 반영 비율을 0.5, 즉 반만 반영하다가 점점 목표치에 도달하게 되면 반영 비율을 높게 증가시켜 주는 것이다.

위 그래프에서 검은색 선은 모멘텀을 적용하지 않았을 때이고, 파란색은 모멘텀을 적용했을 때이다.
모멘텀을 적용하지 않았을 때는 오버슈팅을 확인할 수 있다. 오버슈팅은 이동량이 너무 커서 목표지점을 지나치는 현상을 뜻한다.
모멘텀 - 네스테로프 모멘텀
$$\tilde \Theta = \Theta + \alpha \mathbf v \\
\mathbf v = \alpha \mathbf v - \rho \frac{\partial J}{\partial \Theta}|_{\tilde \theta} \\
\Theta = \Theta + \mathbf v$$
일반 모멘텀과 비교했을 때 네스테로프 모멘텀은 $\mathbf v$로 $\tilde \Theta$를 예측한 후 $\tilde \Theta$에서의 그래디언트로 $\mathbf v$를 누적하고 $\Theta$를 업데이트 한다.

위 그림에서 알 수 있듯이 $\Theta$에서 $\alpha \mathbf v$만큼 이동한 벡터가 $\tilde \theta$이고 $\tilde \theta$에서의 그래디언트만큼 이동한 것이 최종 $\Theta$가 되는 것이다.
적응적 학습률

위 그림에서 검은색 선은 학습률 $\rho$가 높을 때를, 파란색 선은 학습률이 낮을 때를 나타낸 것이다.
학습률이 크면 오버슈팅 현상이 발생해 진자 운동을 할 가능성이 크고 학습률이 작으면 수렴까지의 시간이 오래걸릴 수 있다.
$$\frac{\partial J}{\partial \Theta} = (\frac{\partial J}{\partial \Theta_1}, \frac{\partial J}{\partial \Theta_2}, \cdots,\frac{\partial J}{\partial \Theta_k})^T \\
\rho \frac{\partial J}{\partial \Theta} = (\rho \frac{\partial J}{\partial \Theta_1}, \rho \frac{\partial J}{\partial \Theta_2}, \cdots,\rho \frac{\partial J}{\partial \Theta_k})^T$$
위 식은 그래디언트와 그래디언트에 학습률을 곱한 실제로 업데이트 될 그래디언트 값을 나타낸다.
학습률 $\rho$가 모든 그래디언트에 똑같이 곱해지기 때문에 k개의 매개변수 모두 같은 학습률을 사용한다고 볼 수 있다.
이 때 매개변수마다 학습률을 다르게 적용하는 것을 적응적 학습률이라고 한다. AdaGrad(Adaptive Gradient)와 RMSProp이 있다.
적응적 학습률 - Adagrad
Adagrad 알고리즘
입력 : 훈련집합 $\mathbb X, \mathbb Y$, 학습률 $\rho$
출력 : 최적의 매개변수 $\hat \theta$
1. 난수를 생성하여 초기해 $\theta$를 설정한다.
2. r = 0 // 그레디언트 누적 벡터 초기화
3. repeat
4. 그레디언트 $\mathbf g = \frac{\delta J}{\delta \theta}\vert_{\theta}$를 구한다.
5. $\mathbf r = \mathbf r + \mathbf g \odot \mathbf g$
6. $\Delta \Theta = -\frac{\rho}{\epsilon + \sqrt {\mathbf r}} \odot \mathbf g$
7. $\Theta = \Theta + \Delta \Theta$
8. until (멈춤 조건)
9. $\hat \Theta = \Theta$
라인 5에서 $\mathbf r$은 이전 그래디언트를 서로 곱하여 누적한 벡터이다.
라인 6에서 그래디언트에 $\frac{\rho}{\epsilon + \sqrt r}$이 곱해지는데 이 때 $\mathbf r$이 클수록 이 값은 작아지게 되고 $\mathbf r$이 작을수록 커지게된다.
즉 그래디언트가 크면 줄여주고 작으면 키워주는 역할을 해준다.
적응적 학습률 - RMSProp
AdaGrad의 라인 5에서 모든 단계의 그래디언트들을 같은 비중으로 반영하고있는데, 이는 전역해에 충분히 수렴하지 못한 상황인데도 r이 점점 커지게 되면서 $\Delta \Theta$을 0으로 만들 수 있다는 문제가 있다.
이 문제를 해결하기 위해 오래된 그래디언트의 영향력을 지수적으로 줄이는 가중 이동 평균(Weighted moving average) 기법을 적용한다.
$$\mathbf r = \alpha \mathbf r + (1-\alpha)\mathbf g \odot \mathbf g$$
위 식을 살펴보면 이전 가중치 누적 벡터$\mathbf r$이 계속해서 $\alpha$만큼 반영되고, 현재 그래디언트는 $1-\alpha$만큼 반영된다.
즉 $\mathbf r$을 누적하면 누적할수록 이전의 그래디언트들의 반영 비중은 낮아지게되는 것이다. 보통 $\alpha$는 0.9, 0.99, 0.999와 같은 값을 사용한다.
Adam
아담은 RMSProp에 모멘텀을 추가로 적용한 알고리즘이다. 적응적 학습률에 모멘텀을 추가한 알고리즘인 것이다.
Adam 알고리즘
입력 : 훈련집합 $\mathbb X, Y$, 학습률 $\rho$, 모멘텀 계수 $\alpha_1$, 가중 이동 평균 계수 $\alpha_2$
출력 : 최적의 매개변수 $\hat \Theta$
1. 난수를 생성하여 초기해 $\Theta$를 설정한다.
2. $\mathbf v = 0, \mathbf r = 0$
3. t=1
4. repeat
5. 그레디언트 $\mathbf g = \frac{\delta J}{\delta \Theta}\vert_\Theta$ 를 구한다.
6. $\mathbf v = \alpha_1 \mathbf v - (1 - \alpha_1)\mathbf g$ // 속도 누적 벡터
7. $\mathbf v = \frac{1}{1-(\alpha_1)^t}\mathbf v$
8. $r = \alpha_2 \mathbf r + (1 - \alpha_2)\mathbf g \odot \mathbf g$ // 그레디언트 누적 벡터
9. $\mathbf r = \frac{1}{1-(\alpha_2)^t}r$
10. $\Delta \Theta = - \frac{\rho}{\epsilon + \sqrt{\mathbf r}} \mathbf v$
11. $\Theta = \Theta + \Delta \Theta$
12. $t$++
13. until (멈춤 조건)
14. $\hat \Theta = \Theta$
알고리즘을 살펴보면 속도 벡터 $\mathbf v$를 계산한 후 그래디언트 누적 벡터 $\mathbf r$을 계산한다. 최종적으로
$$\vartriangle \mathbf \Theta = - \frac{\rho}{\epsilon + \sqrt r} \mathbf v $$
이전 학습률과 속도를 반영하여 매개변수를 업데이트 하게 되는 것이다.
활성함수

활성함수는 비선형 함수로 사용한다. 선형 함수를 사용하면 퍼셉트론의 층을 늘려도 결국 선형 방정식의 결과로 표현할 수 있기 때문에 층의 효과가 무의미해지게 되기 때문이다.
그래서 계단 함수와 tanh, ReLU가 순서대로 사용되어왔다. sigmoid와 tanh의 범위는 유사하지만 범위가 [0, 1], [-1, 1]인 차이가 있어 tanh가 우월하다고 입증되었다.
하지만 tanh도 입력값이 커질 수록 1에 근접하게 되는 포화(saturation) 현상이 발생한다.
tanh와 sigmoid의 도함수 모두 종 모양으로 그려지는데, 중심에서 멀어질 수록 도함수의 값은 0에 가까워지게 되고 이는 가중치 소실 문제로 이어져 학습에 큰 지장을 준다.
이 문제를 해결하기 위해 만든 활성 함수가 ReLU이다.
$$z = \mathbf w^T \mathbf {\tilde x} + b \\ y = ReLU(z) = max(0,z)$$
ReLU는 0보다 작은 영역은 0으로 만들고 0보다 큰 영역에서는 선형이다. 음수는 모두 0으로 만들기 때문에 신경망을 희소하게 만드는 효과가 있다고 한다.
신경망이 희소한 상태가 되면 서로 다른 변화 인자를 풀어내는 데 장점이 있다고 여겨진다.
또한 ReLU는 0에서 미분이 불가능한데, 이는 신경망의 분산 구조로 인해 그래디언트가 수많은 경로로 흐르므로 한두 군데에서 미분 불가능한 현상은 실제로 문젯거리가 되지 않는다. ReLU를 응용한 다른 활성함수도 있다.

$$leakyReLU(z) = \begin{cases}z, & z \ge0 \\ az, &z< 0\end{cases} $$
softplus는 전 구간에서 미분이 가능하다는 특징이 있고 leakyReLU와 PReLU는 음수 구간에서의 기울기를 지정할 수 있다는 특징이 있다. PReLU는 기울기 a를 학습한다.
배치 정규화

위 사진에서 x는 처음으로 입력되는 이미지를 의미한다. x는 층을 거칠수록 처음의 분포와 많이 달라지게 된다.
입력 데이터 x의 분포는 일정하지만 층을 거치면 거칠수록 분포의 변화가 커지는 것이다. 이처럼 학습 도중에 샘플의 분포가 바뀌는 현상을 공변량 시프트(covariate shift)라고 한다.
$$z = \mathbf w^T\mathbf {\tilde x} + b \\ y = \tau(z)$$
위 식에서 $\mathbf{\tilde x}$는 직전 층의 출력값을 의미한다. $\mathbf{\tilde x}$에 선형 연산을 적용한 결과값을 $z$, 여기에 활성함수를 적용한 값이 $y$이다.
층을 일반화해서 생각하면 $\mathbf x$와 $y$는 같은 개념의 값들이다. 현재 층의 출력값 $y$가 다음 층의 입력($\mathbf x$)으로 들어가기 때문이다.
그렇다면 $\mathbf x$와 $z$중 배치 정규화는 어디에 적용해야 할까? 실험을 근거로 배치 정규화는 아직 활성함수를 거치지 않은 $z$에 적용한다.
다음은 배치 단위로 정규화를 진행하는 과정을 나타낸 것이다.
$$\mu_B = \frac{1}{m}\sum_{i=1}^mz_i \\
\sigma_B^2 = \frac{1}{m}\sum_{i=1}^m(z_i-\mu_B)^2 \\
\tilde z_i = \frac{z_i -\mu_B}{\sqrt{\sigma^2_B+\epsilon}}, \ \ \ \ i=1,2,\cdots,m \\
z'_i=\gamma \tilde z_i + \beta$$
배치 사이즈 만큼의 데이터들에 대해 평균($\mu_B$)과 표준편차($\sigma^2_B$)를 구하고 구해진 평균과 표준편차로 배치 이미지들의 정규화를 진행한다.
그리고 $\gamma$, $\beta$의 매개변수로 이루어진 선형 변환을 거쳐 반환된 $z'_i$를 활성함수의 입력값으로 넣는 것이다.
이처럼 $z_i$를 $z'_i$로 변환하는 것이 배치 정규화의 핵심이다. $\gamma$, $\beta$는 학습으로 알아내야 한다.
배치 정규화 식에서 마지막 식을 추가한 이유는 정규화 과정이 시그모이드 함수의 비선형성을 억제할 수 있기 때문이다.
'공부' 카테고리의 다른 글
| [딥러닝 공부] 딥러닝 최적화4 - 하이퍼 파라미터 최적화 (5) | 2025.01.03 |
|---|---|
| [딥러닝 공부] 딥러닝 최적화3 - 규제 기법, 하이퍼 파라미터 최적화 (0) | 2025.01.03 |
| [딥러닝 공부] 딥러닝 최적화1 - 목적 함수 (0) | 2025.01.03 |
| [딥러닝 공부] 딥러닝 기초(다층 퍼셉트론 오류 역전파 이론) (2) | 2025.01.02 |
| [딥러닝 공부] 노이즈 제거를 위한 이미지 필터링(평균, 미디언, 가우시안) (7) | 2025.01.02 |




