| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- google summer of code
- Object detection article
- res
- 1차 미분 마스크
- 딥러닝 엔트로피
- TransFuser
- 객체 검출
- E2E 자율주행
- vlm
- 논문 리뷰
- clip adapter
- 원격 학습 안끊기게
- mobilenetv1
- 에지 검출
- blip-2
- res paper
- 논문 요약
- gsoc 2025
- gsoc
- referring expression segmentation
- transfuser++
- gres
- gsoc 후기
- object detection
- clip
- 딥러닝 목적함수
- grefcoco dataset
- 이미지 필터링
- 엔트로피란
- grefcoco
- Today
- Total
My Vision, Computer Vision
[논문 요약/리뷰] Talking to DINO: Bridging Self-Supervised Vision Backbones with Language for Open-Vocabulary Segmentation 본문
[논문 요약/리뷰] Talking to DINO: Bridging Self-Supervised Vision Backbones with Language for Open-Vocabulary Segmentation
gyuilLim 2025. 5. 2. 19:43Talking to DINO: Bridging Self-Supervised Vision Backbones with Language for Open-Vocabulary Segmentation
Open-Vocabulary Segmentation (OVS) aims at segmenting images from free-form textual concepts without predefined training classes. While existing vision-language models such as CLIP can generate segmentation masks by leveraging coarse spatial information fr
arxiv.org
Author : Barsellotti, Luca, et al.
Journal : Arxiv
Keyword : Open-Vocabulary, Segmentation
Published Date : 2024년 11월 28일
Problem
- CLIP 기반 백본은 강력한 Cross-Modal 능력을 갖고있음에도 불구하고 이미지와 텍스트의 전역적인 유사도를 예측하는 방식으로 사전학습 됐기 때문에 공간적인 예측 능력, 특히 Dense Prediction은 부족하다.
- 따라서 세밀한 특징과 공간적 정보를 잘 포착하는 Self-Supervised Vision-Only Backbone인 DINOv2를 활용한다.
- DINO 계열 모델은 Self-Distillation Loss와 패치 수준 특징 학습, Self-Supervision으로 학습되고 Self-Attention을 사용하기 때문에 의미론적 정보 및 전경(Foreground)의 지역적인 정보를 가지고 있을 것이다라는 주장이다.
Contributions
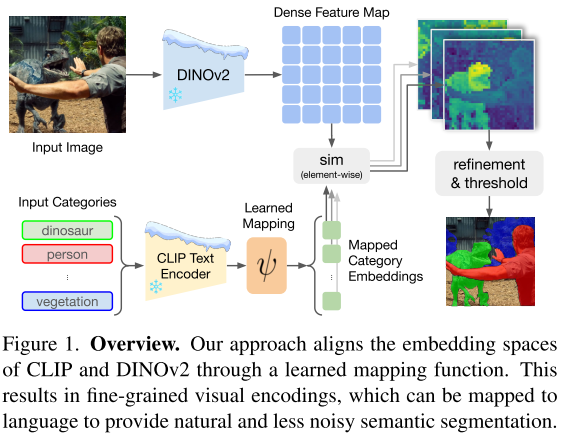
- DINOv2와 CLIP의 Textual 임베딩을 Align하는 모델인 Talk2DINO를 제안한다.
- 백본을 파인튜닝할 필요 없는 Training Schema를 제안한다.
Methods
Preliminaries
- 입력 이미지($I$) : $I \in \mathbb R^{H\times W\times 3}$
- Visual Backbone에서 추출된 Dense Feature Map($v(I)$) : $v(I) \in \mathbb R^{\frac{H}{P} \times \frac{W}{P} \times D_v}$. 이 때, $P$는 패치 크기, $D_v$는 임베딩 차원
- M개의 텍스트 카테고리 집합 : ${T_j } _{j=1, \dots M}$, 각 텍스트 피쳐는 $t(T_j) \in \mathbb R^{D_t}$ 차원을 가진다.
- 또한 간소화를 위해 $v(I)$는 $v$, $t(T_j)$는 $t_j$로 표기한다.
- 멀티모달 학습의 경우 $D_v = D_t$ 이다. 따라서 $I$ 와 $T_j$ 사이 Attention Map($S(I, T_j)$)을 계산할 수 있다. 이 때 $S(I,T_j) \in \mathbb R^{\frac{H}{P} \times \frac{W}{P}}$ 이다.
$$ S(I,T_j){[h,w]} = \frac{v{[h,w]} \cdot t^T_j}{||v_{[h,w]}||\ ||t_j||} $$
- 이후 $S(I,T)$를 업샘플링하여 원래의 해상도로 복원한 $\hat S(I,T)$를 만들고 Argmax를 취하여 Segmentation Mask를 생성한다.
$$ \mathcal M(I, T_1, \dots, T_M){[h, w]} = \textrm{argmax}{j=1, \dots, M} \mathcal S(I,T_j)_{[h, w]} $$
Augmenting DINO with Semantics
Warping CLIP Embedding Space
- 텍스트 임베딩을 DINOv2의 패치 임베딩 공간으로 투영시키기 위해 매핑함수 $\psi$ 를 사용한다.
- 식으로 나타내면 아래와 같다.
$$ \psi(t) = \mathbf W^T_b(\textrm {tanh}(\mathbf W^T_a t + b_a))+b_b $$
- $\mathbf W_a \in \mathbb R^{D_t \times D_v}$ 이고, $\mathbf W_b \in \mathbb R^{D_v \times D_v}$ 이다.
Mapping DINO to the Warped CLIP Space

- $\psi$를 학습시키기 위해 DINOv2의 고유한 Segmentation 능력을 활용하여 $\psi(t)$ 와 $v$ 를 정렬시킨다.
- 먼저 CLS vector $v^*$ 와 패치 특징 $v$ 간에 Attention을 계산하고, N개의 헤드에서 어텐션맵 $A_i \in \mathbb R^{\frac{H}{P} \times \frac{W}{P}}$ 을 추출한다.
- 그 후 각 $A_i$에 대해 $v$ 를 곱하여 가중치를 부여한다. $v \cdot \textrm {softmax}(A_i) \in \mathbb R^{\frac{H}{P} \times \frac{W}{P} \times D_v}$
- 이어서 차원별 평균을 계산하여 최종적으로 $v^{A_i} \in \mathbb R^{D_v}$ 를 구하고 $\psi(t)$ 간 코사인 유사도를 계산하여 총 N개의 유사도 점수를 얻는다.
- 각 헤드와 텍스트 임베딩 간 코사인 유사도는 다음과 같이 정의된다.
$$ \textrm {sim}(v^A_i, t) = \frac{v^{A_i}\cdot \psi(t)^T}{||v^{A_i}||\ ||\psi(t)||} $$
- 여기서 $v^{A_i}$ 는 다음과 같이 정의된다.
$$ v^{A_i} = \sum_{h,w}v_{[h,w]} \textrm{softmax}(A_i)_{[h,w]} \in \mathbb R^{D_v} $$
- 이렇게 N개의 헤드에서 얻어진 유사도 점수 중 가장 큰 유사도를 가지는 특징만 정렬에 반영하는 것이다.
Experiment

- Open-Vocabulary Segmentation 벤치마크에 대한 성능 측정 결과




